[最も好ましい] 多角形内角 141129-多角形内角求め方
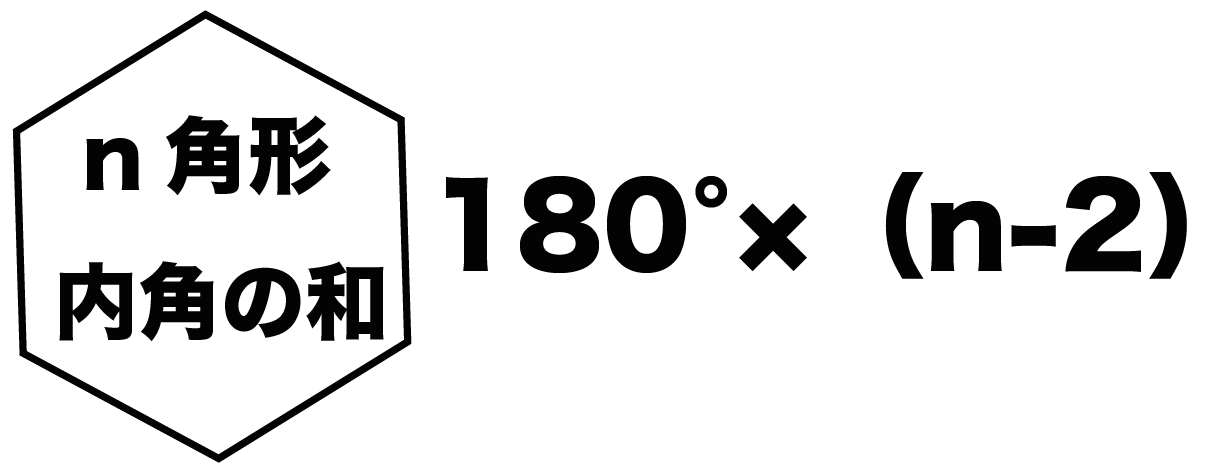
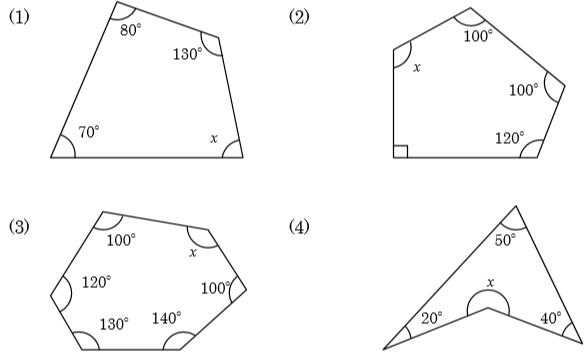
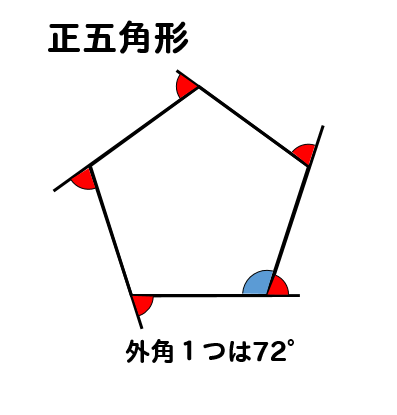
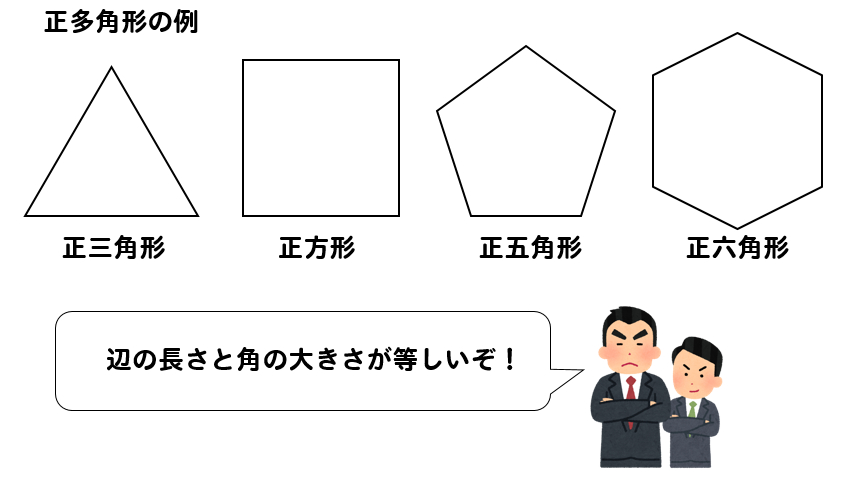
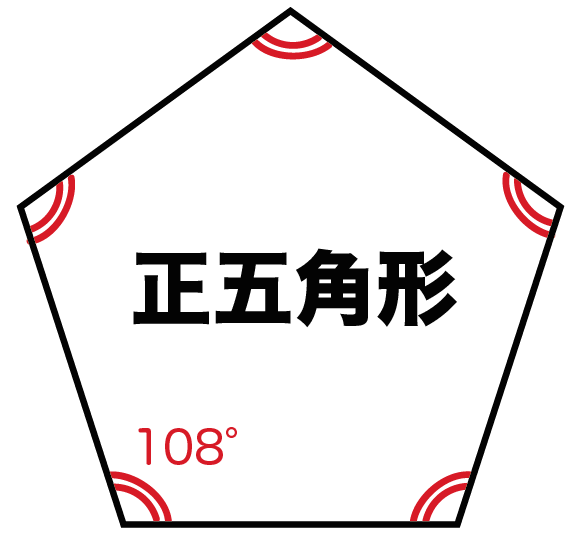
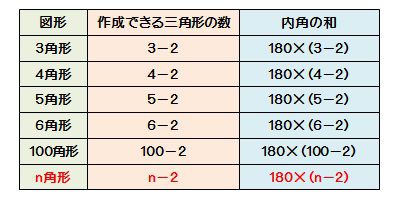
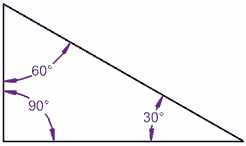
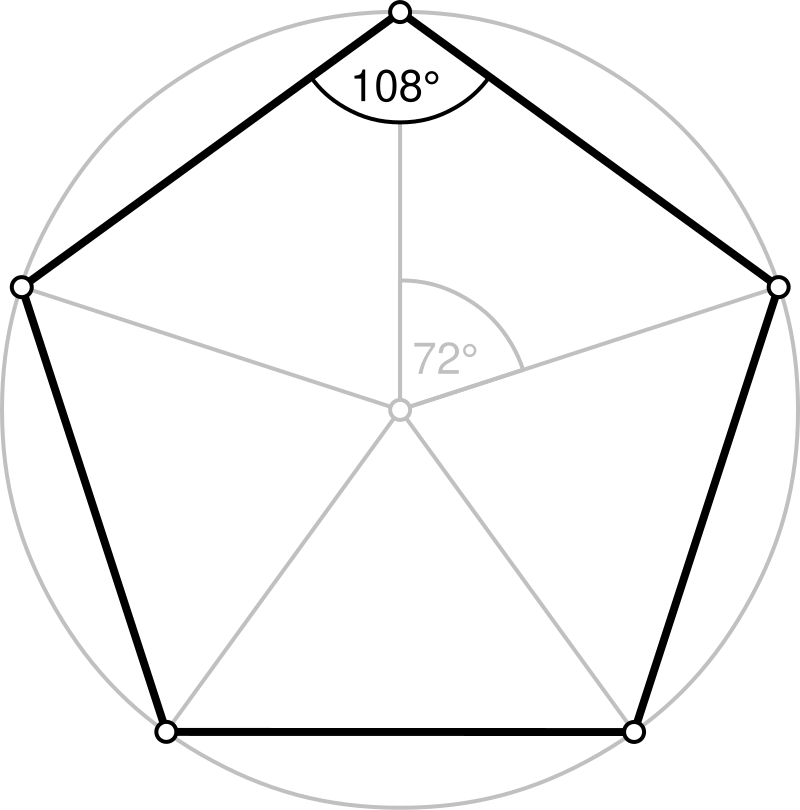
多角形の内角の和は 180°×(n−2) 正多角形のすべての内角の大きさは等しいから,正n角形の1つの内角の大きさは =180°− 例 • 正三角形 外角= =1° 内角= 180°−1° =60° • 正方形 外角= =90° 内角= 180°−90° =90° • 正五角形 外角= =72° 内角= 180°−72° =108° 問題 2 1 x の大きさを求めなさい x
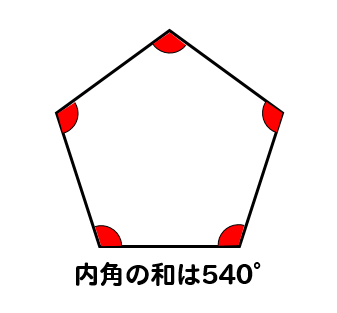
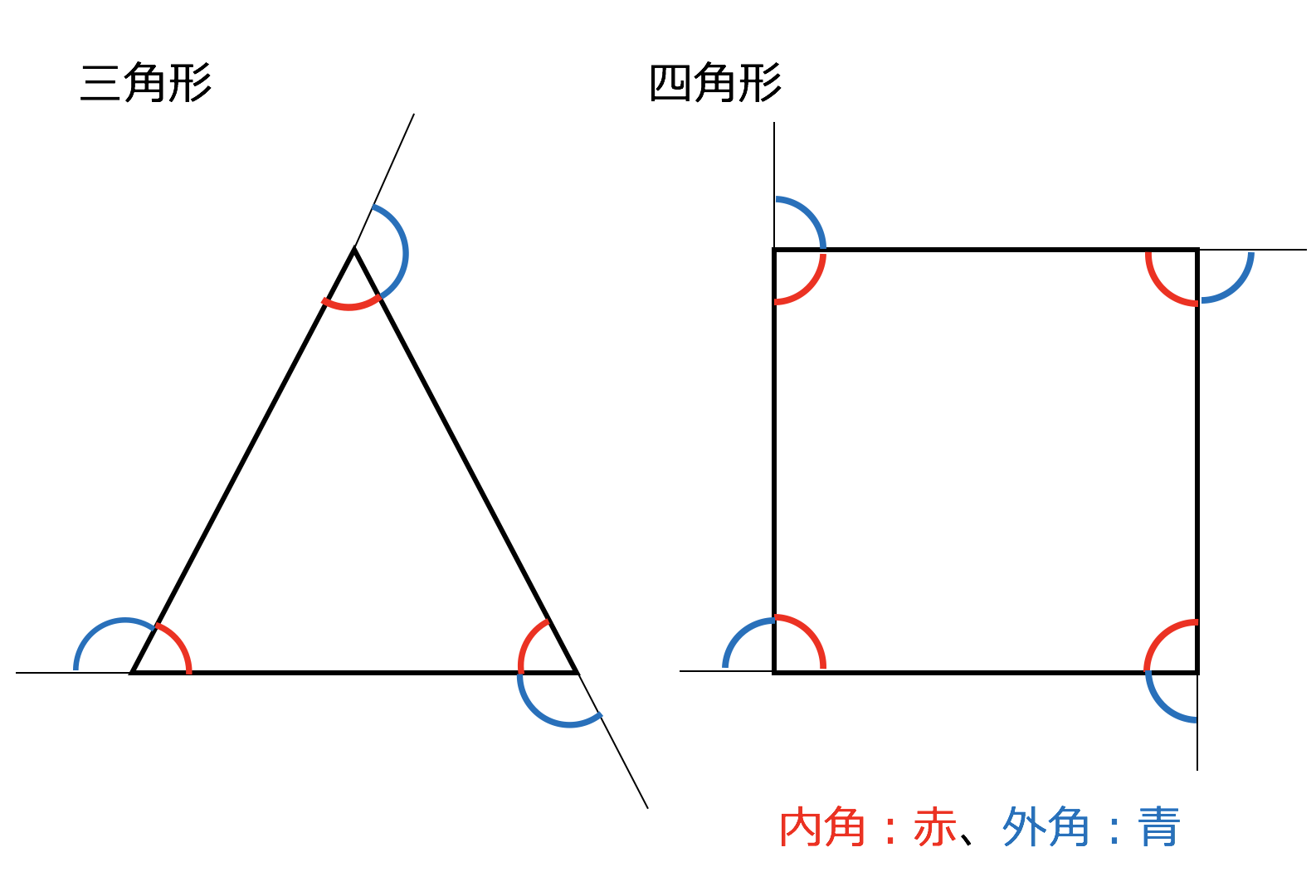
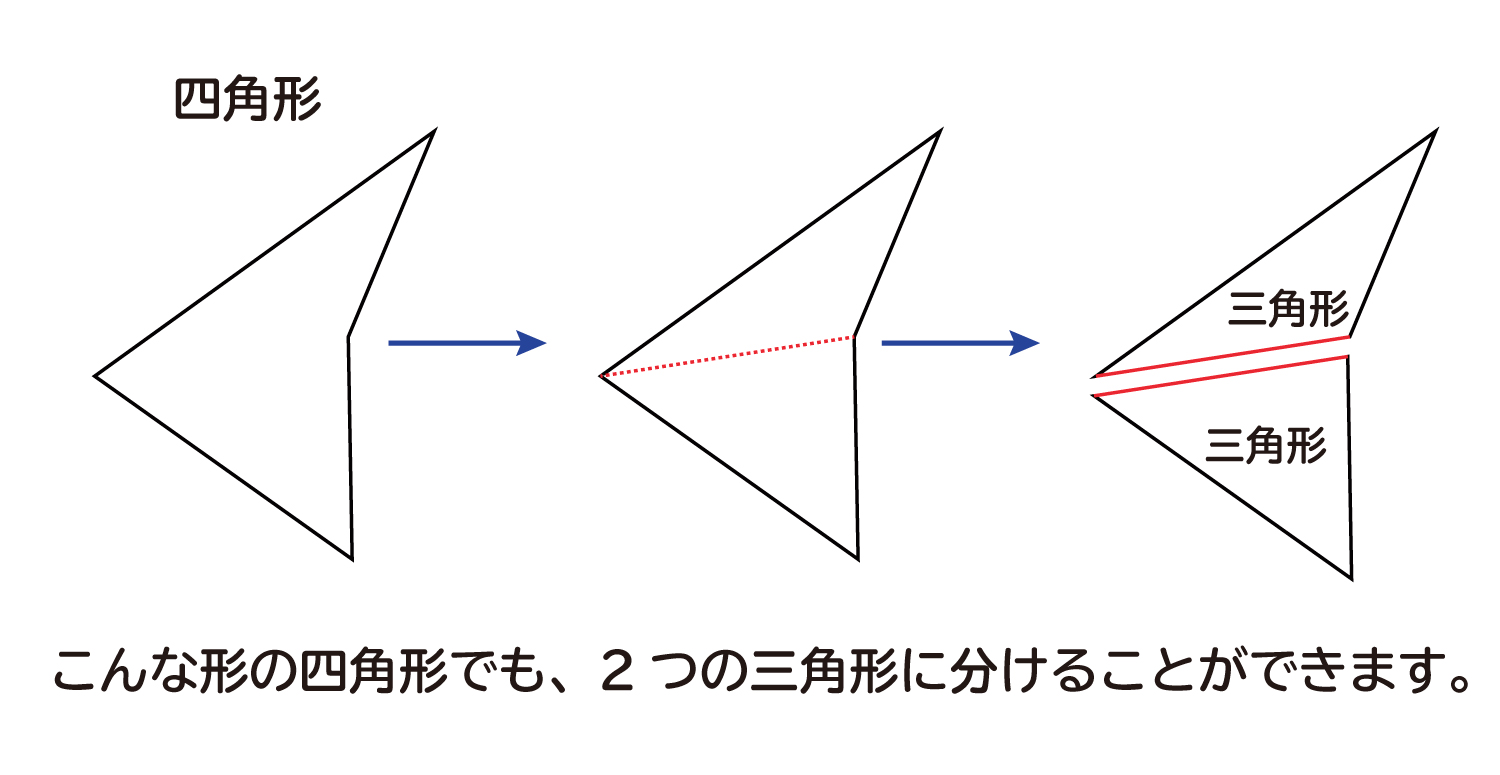
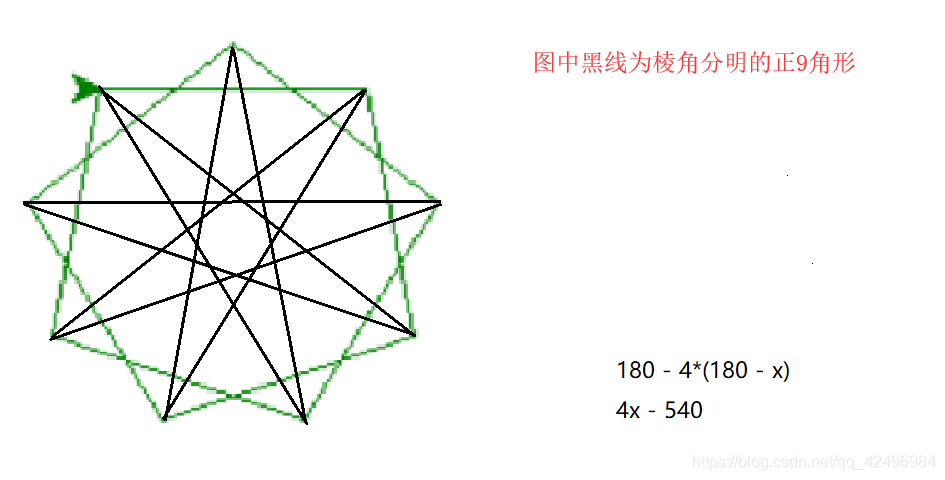
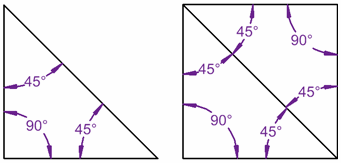
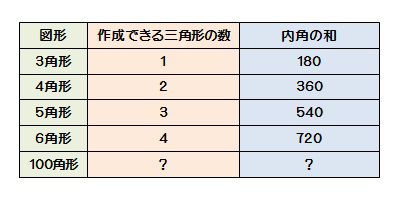
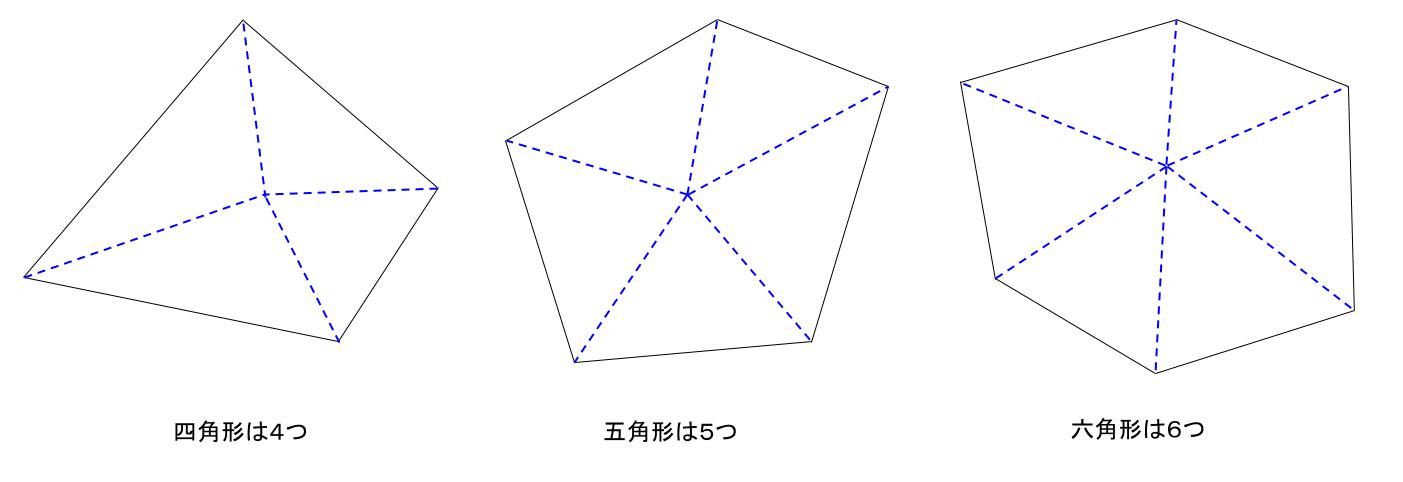
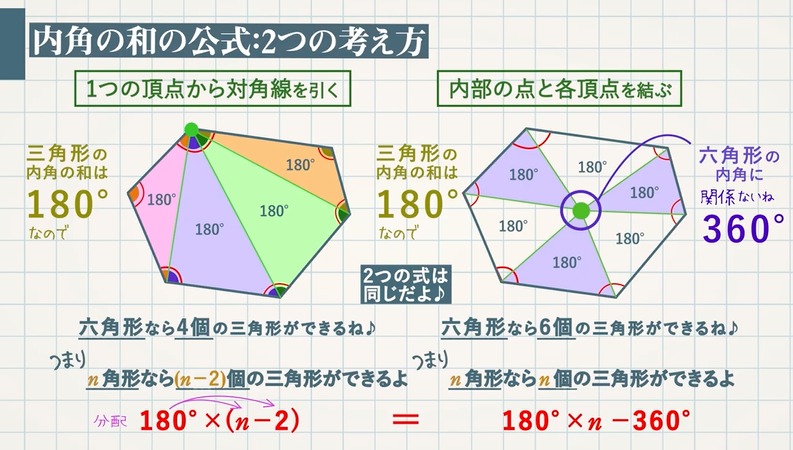
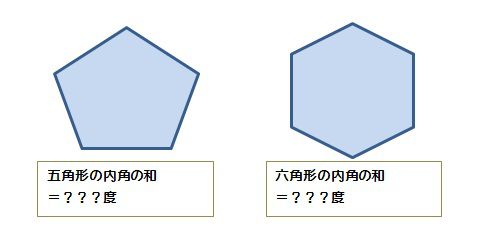
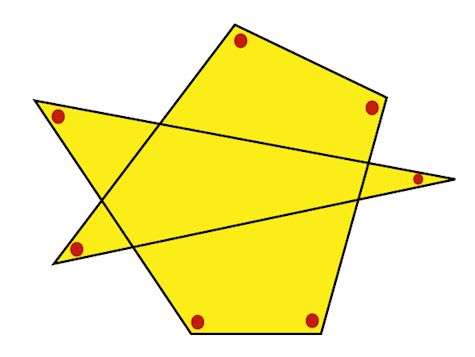
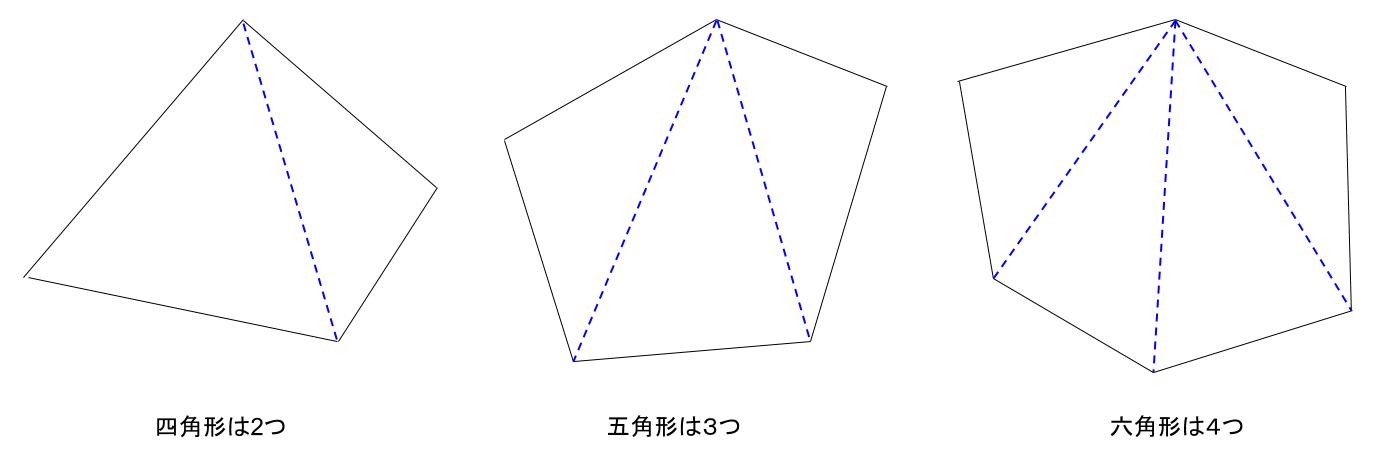
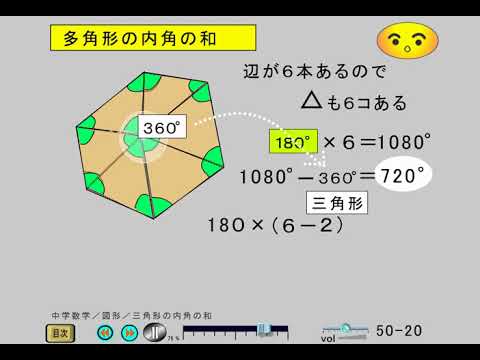
多角形内角求め方- 多角形の1つの角の内角と外角の和は180°です。 Adding the sum of the angles in a triangle one after another gives us the sum if the interior angles in a polygon 三角形の角度の和を次々に足していけば、多角形の内角の和が求められます。 Dividing a regular hexagon by its diagonals, we get six equilateral triangles 正六角形を対角線で内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い
多角形内角求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  |  |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 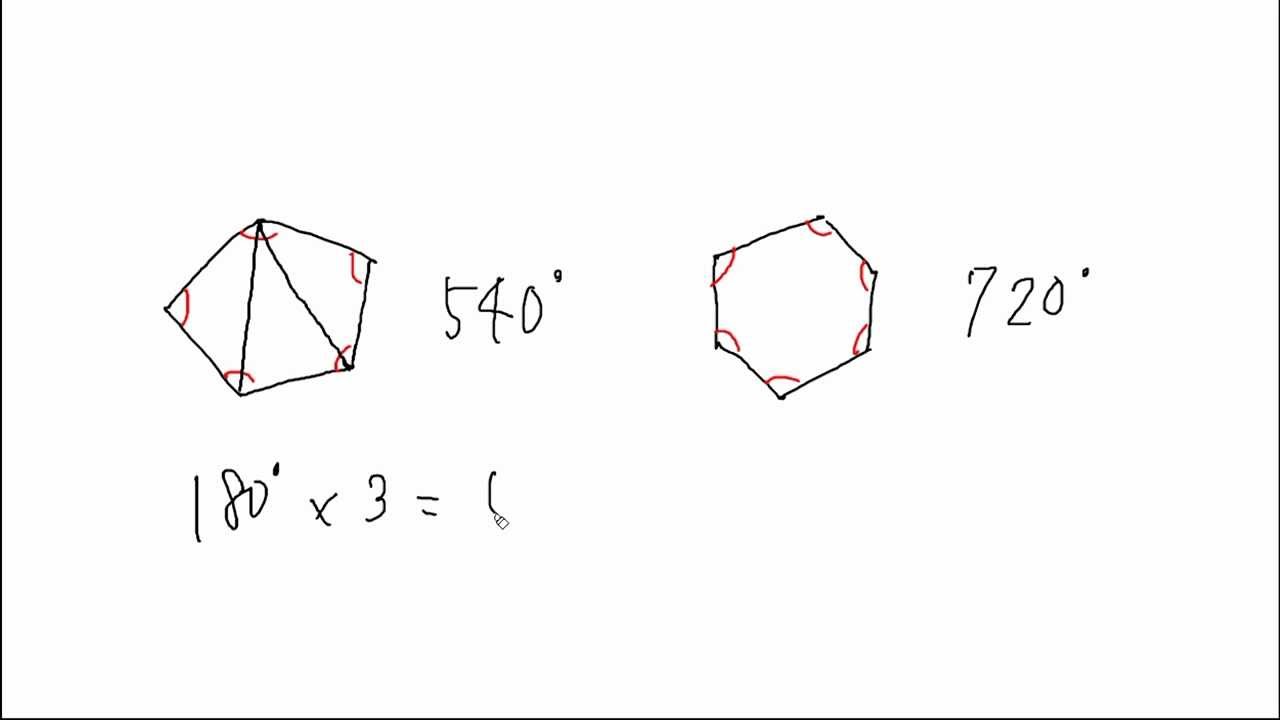 |  |
 |  |  |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 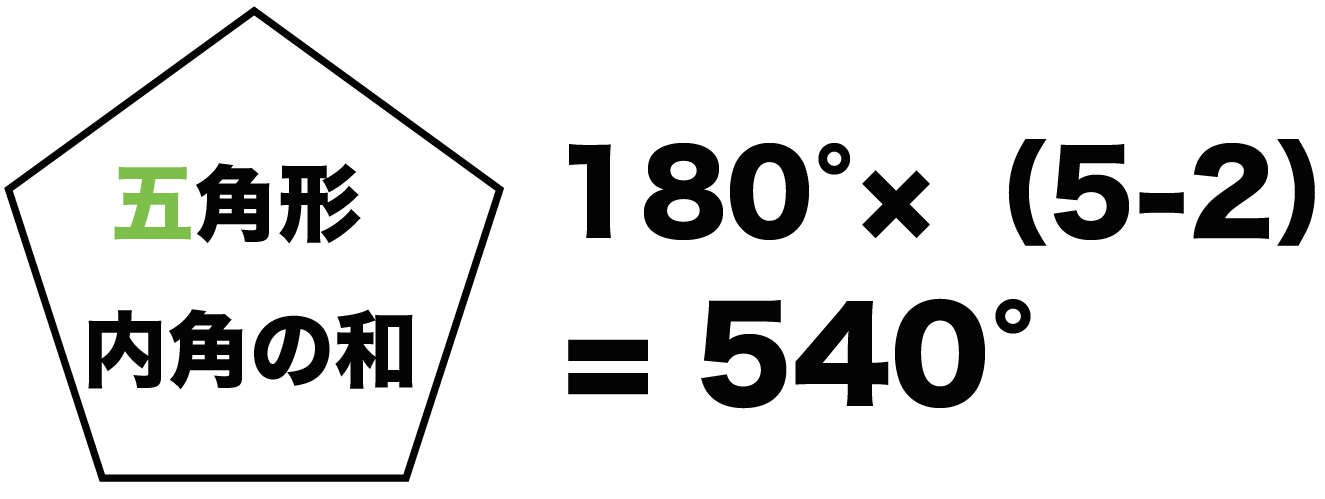 |  |
 |  |  |
 |  | |
「多角形内角求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
多角形の基本は内角和と外角和 チートシートを使いながら、多角形の性質について親子で流れで整理してみました。 まずは、多角形の1つの頂点から対角線を引くと点の数から3を引いた「n3」になります。 点はそれ自身に線を引くことができず、両どなりの2点には辺しか描けないからで三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.
Incoming Term: 多角形内角の和, 多角形内角求め方, 多角形内角,
コメント
コメントを投稿